References
[1]. Aczel, A. D. (1996). Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem. N. Y.:Dell
Publishing.
[2]. Boston, N. (1995). A Taylor-made plug for Wiles' proof. The College Mathematics Journal, 26(2), 100-105.
[3]. Cornell, G., Silverman, J., and Stevens, G., (eds.) (1997). Modular Forms and Fermat's Last Theorem. Springer-
Verlag.
[4]. Granville, A., & Monagan, M. B. (1988). The first case of Fermat's last theorem is true for all prime exponents up to
714,591,416,091,389. Transactions of the American Mathematical Society, 306(1), 329-359.
[5]. Ireland, K., & Rosen, M. (1990). A Classical Introduction to Modern Number Theory (Vol. 84). Springer Science & Business
Media.
nd [6]. Jacobson, N. (1989). Basic Algebra II, 2 Ed. New York: W. H. Freeman.
[7]. Kumar, V. (2010). Restricted backtracked algorithm for Hamiltonian circuit in undirected graph. BIJIT-BVICAM's
International Journal of Information Technology, 2(2), 23-32.
[8]. Kumar, V. (2012). Mathematics Is Science: A topic revisited in context of FCS of India. International Journal of Modern
Education and Computer Science, 4(6), 17-26.
[9]. Kumar, V. (2014). Proof of Fermat last theorem based on odd even classification of integers. Int. J. Open Problems
Compt. Math., 7(4), 23-34.
[10]. Kumar, V., (2015). Discrete Mathematics. New Delhi: BPB Publication.
[11]. Mauldin, R. D. (1997). A generalization of Fermat's Last Theorem: The Beal conjecture and prize problem. Notices of the
American Mathematical Society, 44(11), 1436-1437.
[12]. Radford, L., & Peirce, C. S. (2006, November). Algebraic thinking and the generalization of patterns: A semiotic
th perspective. In Proceedings of the 28 Conference of the International Group for the Psychology of Mathematics
Education, North American Chapter (Vol. 1, pp. 2-21).
[13]. Ribenboim, P. (1999). Fermat's Last Theorem for Amateurs. New York: Springer-Verlag.
[14]. Rubin, K., & Silverberg, A. (1994). A report on Wiles' Cambridge lectures. Bulletin of the American Mathematical
Society, 31(1), 15-38.
[15]. Silverman, J. H. (1986). Heights and elliptic curves. In Arithmetic Geometry (pp. 253-265). Springer, New York, NY.
rd [16]. Stewart, I., & Tall, D. (2002). Algebraic Number Theory and Fermat's Last Theorem, 3 Ed. AK Peters/CRC Press.
[17]. Washington, L. C. (1997). Introduction to Cyclotomic Fields (Vol. 83). Springer Science & Business Media.
[18]. Wiles, A. (1995). Modular elliptic curves and Fermat's last theorem. Annals of Mathematics, 141(3), 443-551.
[19]. Zelator, K. (2011). Integer Roots of Quadratic and Cubic Polynomials with Integer Coefficients. arXiv preprint
arXiv:1110.6110.
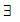 no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
">
no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
">
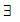 no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.